Pentagramm-Rätsel in Prolog lösen

Prolog ist eine Programmiersprache für Programmierung in Logik. Damit lassen sich bspw. auch Knobelaufgaben relativ einfach programmieren und lösen.

Das Rätsel

Ein Beispiel ist die Knobelaufgabe, um die freien Stellen auf einem Pentagramm so mit vorgegebenen Zahlen zu befüllen, so daß die Zahlen auf allen Linien die gleiche Summe ergeben:

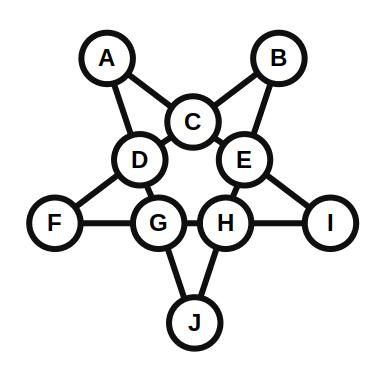
Für die vorgegebenen Zahlen 1, 2, 3, 4, 5, 6, 8, 9, 10, und 12 müssen die Summen der Zahlen auf den einzelnen Linien 24 ergeben, also A+D+G+J, A+C+E+I, B+C+D+F und B+E+H+J. Diese der vorgegebenen Zahlen darf und muß genau einmal eingesetzt werden.

Der Programmcode

In Prolog lässt sich das Rätsel sehr einfach implementieren:

puzzle(Vs, S, P) :-
    % Determine permutations
    permutation(Vs, P),
    
    % Split permutation into single values
    P = [A,B,C,D,E,F,G,H,I,J],

    % Check first sum
    S =:= A + D + G + J,

    % Check second sum
    S =:= A + C + E + I,

    % Check third sum
    S =:= B + C + D + F,

    % Check fourth sum
    S =:= B + E + H + J.

puzzle ermittelt die Lösung des Rätsels.

Ausgenutzt wird hier die Tatsache, daß die Lösung eine Permutation der vorgegebenen Werte sein muß. Prolog geht alle möglichen Permutation durch und prüft auf die eingesetzten Werte auf die Summe 24.

Die Abfrage für die Lösung des Rätsel ist

?-puzzle([1,2,3,4,5,6,8,9,10,12], 24, P).

Prolog ermittelt die Lösung des Rätsels und liefert

P = [1, 2, 4, 12, 9, 6, 3, 5, 10, 8]

liefert aber noch weitere Ergebnisse, bspw.

P = [1, 2, 8, 9, 12, 5, 10, 6, 3, 4]
P = [1, 2, 9, 8, 4, 5, 3, 6, 10, 12]
P = [1, 2, 12, 4, 8, 6, 10, 5, 3, 9]
P = [1, 5, 3, 10, 8, 6, 4, 2, 12, 9]
P = [1, 5, 8, 9, 3, 2, 4, 6, 12, 10]

Rätsel generieren

Mit dem gleichen Code lässt sich auch ein neues Rätsel generieren, bzw. prüfen, ob es eine gemeinsame Summe für eine Reihe von vorgegebenen Zahlen gibt.

Für die Zahlen von 1 bis 10 liefert Prolog Lösungen u.a. für die Summen 20 und 21:

?-puzzle([1,2,3,4,5,6,7,8,9,10], S, P).
P = [1, 3, 2, 9, 8, 7, 5, 4, 10, 6],
S = 21

P = [1, 4, 2, 5, 7, 9, 8, 3, 10, 6],
S = 20

Keine Lösung gibt es für die Zahlen von 1 bis 9 und 30:

?-puzzle([1,2,3,4,5,6,7,8,9,30], S, P).
false